Scientific Machine Learning (SciML)
Scientific Machine Learning (SciML) is an interdisciplinary field that merges the principles of physics-based modeling with data-driven techniques like Machine Learning (ML) and Deep Learning (DL). In our lab, the research topic on SciML is coordinated by Prof. Salvatore Cuomo, who leads the efforts in advancing this cutting-edge area of study.
What are Physics-Informed Neural Networks (PINNs)?
A key methodology within SciML is the use of Physics-Informed Neural Networks (PINNs). PINNs combine the power of deep learning with the governing equations of physical systems, allowing us to model complex phenomena without the need for traditional mesh-based methods. By integrating physical laws directly into the neural network’s architecture, PINNs are capable of solving both forward and inverse problems across various domains.
PINNs work by minimizing a loss function that takes into account the physical equations (such as Partial Differential Equations) and boundary conditions. This approach allows us to generate solutions that are not only accurate but also consistent with the underlying physics, even when data is limited.
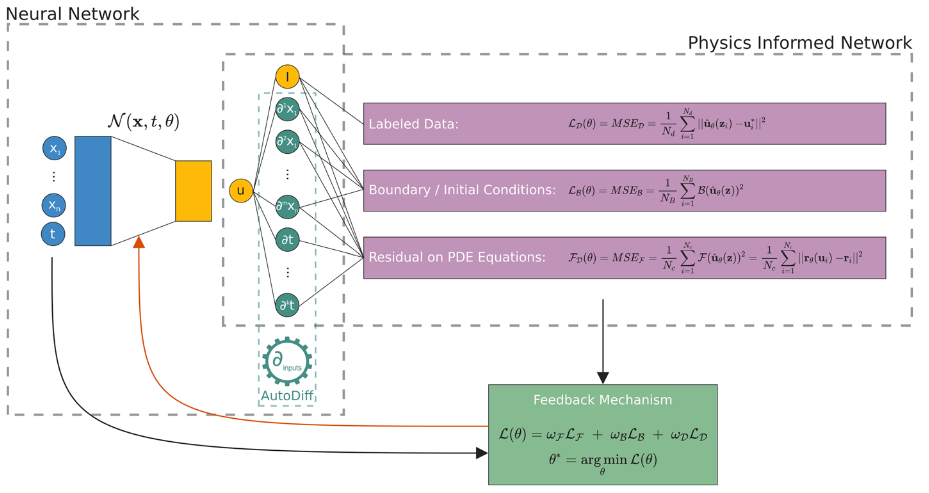
Our Research Achievements
Our research team has applied PINNs to numerous fields, demonstrating the flexibility and power of this approach. Below are some highlights of our applications:
1. Free Boundary Problems
We have successfully used PINNs to solve challenging free boundary problems, particularly in the context of fluid dynamics. These problems, which involve unknown boundaries, are notoriously difficult for traditional methods. With PINNs, we are able to accurately approximate these boundaries and provide solutions with higher precision.
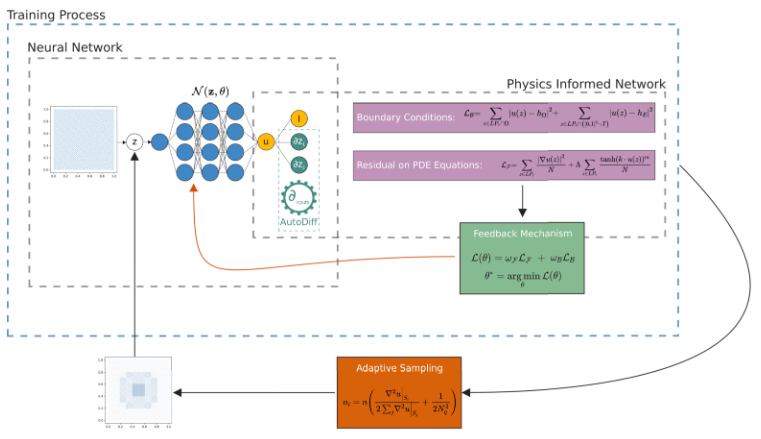
2. Multi-Asset Option Pricing in Finance
In the financial sector, we applied PINNs to address the pricing of American multi-asset options, which pose significant challenges due to their free boundary nature and path dependency. By using a meshless PINN-based approach, we have achieved greater accuracy and efficiency in predicting option prices compared to conventional methods.
3. Groundwater Flow Simulation
We have also applied PINNs to environmental modeling, particularly for simulating groundwater flow through porous media. Traditional methods like the Finite Difference Method (FDM) struggle with such complex simulations, but PINNs offer a more efficient and accurate solution, especially in higher dimensions.
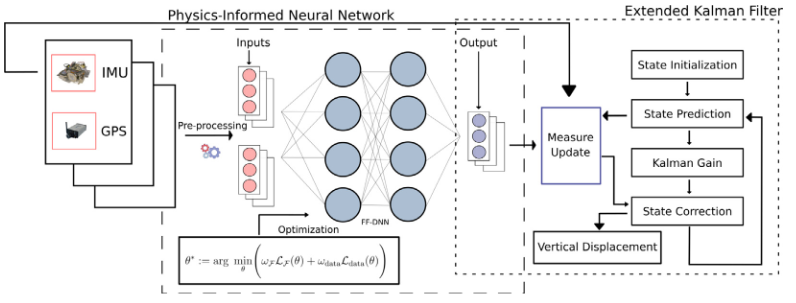
4. Railway Infrastructure Monitoring
PINNs have proven highly effective in monitoring railway infrastructure. By integrating them with sensor data and Kalman Filters, we can predict vertical displacement with high accuracy, helping prevent potential derailments and structural issues.
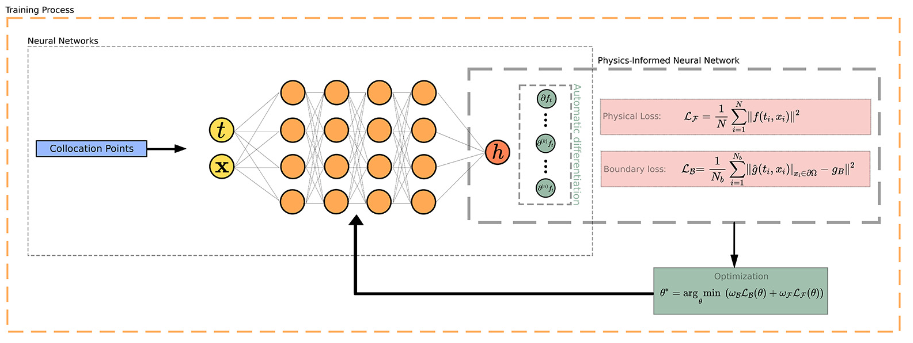
Our Landmark Survey
In addition to our application-driven research, we have also conducted an extensive survey on the use of Physics-Informed Neural Networks in Scientific Machine Learning. This survey has become a key reference in the field, with over 1100 citations, highlighting its impact and the growing relevance of PINNs in solving real-world problems.
Why Choose PINNs?
- Mesh-Free Methods: PINNs do not require the generation of computational meshes, which simplifies their application to complex, high-dimensional problems.
- Data Efficiency: Because PINNs incorporate physical laws directly, they require fewer data points compared to traditional purely data-driven approaches.
- Versatility: PINNs can be applied across many domains, from finance to environmental modeling, making them a powerful tool for solving both forward and inverse problems.
Future Directions
Moving forward, we are expanding the application of PINNs to include real-time monitoring systems for smart cities and autonomous vehicles. We are also developing hybrid models that combine domain-specific physical laws with machine learning techniques to push the boundaries of what is possible in scientific computing.
